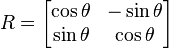Same Analysis with description and Source Code Given Here
Category: C Programming
Animation and The Role of GPU – A Performance factor
Animation and The Role of GPU – A Performance factor
Just take a look into the given CSS which rotates your div by 360deg
.box_rotate {
-webkit-transform: rotate(360deg);
-moz-transform: rotate(360deg);
-ms-transform: rotate(360deg);
-o-transform: rotate(360deg);
transform: rotate(360deg);
}
Code Example – JSFiddle
Have you ever wondered what happens in your computer when we see even a simple animation?
Your computer algorithm calculates every pixel and performs CPU intensive operation over each pixel. Ok what such operations it does ?. It calculates every pixel and performs Discrete Fourier Transformation on each pixel of the image. If your image is 512X512 = 2,62,144 pixels and the algorithms operates several frames per second, like 50 frames per second which depends upon the type of hardware/algorithm being used. It operates every pixel several times per second ( like every pixel 60 times per second ) now image for an image with size 512X512 = 2,62,144pixels and each pixel operated 60 times per second this gives you unbelievably huge number.
Assume that you operated only 1 second,
2,62,144 * 60 = 1,57,28,640 times and these many times it is not just a simple operation, they may apply Fourier transformation on each pixel.
Another important factor to note that the Image rotation, Image scaling or any graphics related operations the the matrix calculations will come into picture. The rotation matrix and the image matrix will be multiplied to get the resulting image
An image matrix will be a huge one, like 512 x 512 x 3 for a given 512X512 image. the 3 in matrix indicates image is RGB coloured. It is not required to explain how matrix multiplications are CPU extensive, Theoretically, matrix-matrix multiplication uses O(N^3) operations on O(N^2) data.
Comparison of GPU Matrix Multiplication operation over CPU
Why GPU and Why not CPU.
GPU are specifically made for performing graphics operations like moving pixels and applying transforms. Since CPU will be doing many more tasks like file operations, audio, calculations etc it is better to separate out your animated objects and give it to a different GPU layer. Imagine in the screen of 1024X800, somewhere some 200X100 size portion is animating, rather than giving 1024X800 space and find 200×100 space and then operate , it is nice trick to create separate layer of 200×100 space and perform animation independently in that layer.
So the load on your CPU will be reduced and the performance of the system will be improved. The difference between CSS3 and jquery animations are , CSS3 utilises GPU but jquery doesn’t, there another javascript based latest framework available called GSAP which is 20x faster than query.
Comparison of jquery, CSS and GSAP Animation Performance :
http://codepen.io/GreenSock/pen/srfxA
Check our another article – how-to-make-you-web-site-faster-html-javascript-tricks
Reference : https://css-tricks.com/myth-busting-css-animations-vs-javascript/
For loop VS While Loop – which is faster ?
Many times I have come across a very basic question Whether For loop is faster ? or While loop is faster in C and other languages. Most of the times an unexperienced developers use to ask this question to me. So I thought to write an article on this .
The answer to this question is – there are no difference in performance , both For and While loop perform same , but this may differ a little for different compilers. It may slightly differ for different compilers because it depends on how a compiler compiles and generates machine code for the same. Even thought those factors are negligible .
I managed to figure it out by looking into the intermediate assembly code generated for both For loop and while loop. Looking at the assembly instructions generated for both , it shows that both have similarly equal number of instructions and similar instructions.
Instead of explaining it in text, I am posting screenshot of assembly code generated with marking of details. The assembly code is generated in Mac OS X , XCode by using Assemble option.
Recursion VS Iteration – An Analysis with fibonacci and factorial
Recursion VS Iteration – An Analysis with fibonacci and factorial
It is always difficult to choose one over the other , but recursive and iterative methods can be chosen wisely by analysing the algorithm with certain input values. Let us study the usage of recursive methods and let us analyse how recursive call works internally.
How Recursion Works ?
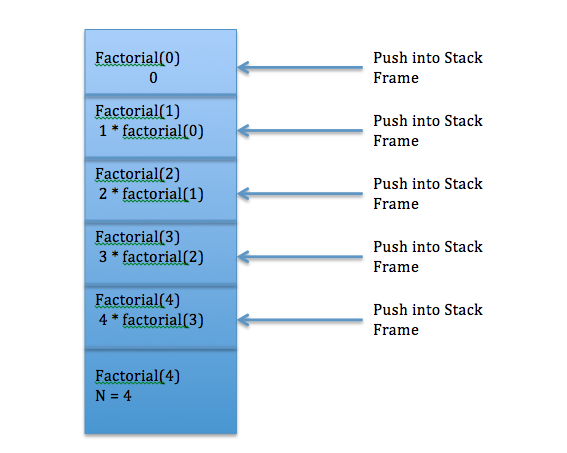
The concept of stack frame comes into picture when we deal with recursion, for each call a stack frame will be created and the values will be pushed into stack. Once the recursive call reach the final condition, the program will start popping out from the stack frame and returns the values . A C program to find factorial of given number and analyse it using recursive method.
Let us take an example –
Finding Factorial of a Number
long int count = 1;
long int factorial(long int n){
count++;//to count how many times the method getting called
if (n == 0) {
return 1;
}
return n * factorial(n - 1);
}
int main(int argc, const char * argv[])
{
int n = 13;
printf("Factorial of %d = %lu , number of time called %lu\n",n,factorial(n),count);
return 0;
}
Let Analyse how it works ?
When factorial(n) will be called every time , a stack frame will be created and the call will be pushed to stack, the entire call stack looks like below. The below image shows stack operations for a given recursive call.
If I give input as 10, the recursive method will be called 12 times,
If I give input as 14, the recursive method will be called 16 times,
If I generalise the number time of call then it will be – n + 2 times.
This looks ok, but let us take different example and try to compare both. A program to find fibonacci number and analyse it with respect to call stack.
Finding Fibonacci number
long int count = 1;
long int fibonacci(int n){
count++;
if (n <= 1) {
return n;
}else{
return fibonacci(n-1) + fibonacci(n - 2);
}
}
long int fibonacciIteration(int n) {
int x = 0, y = 1, z = 1;
for (int i = 0; i < n; i++) {
x = y;
y = z;
z = x + y;
}
return x;
}
int main(int argc, const char * argv[])
{
int n = 4;
printf("fib value recursive %lu ",fibonacci(n));
n = 100; // let us give 100 as input for iterative method
printf("\nIterative method %lu ",fibonacciIteration(100));
printf("\nnumber of time called %lu\n",count);
return 0;
}
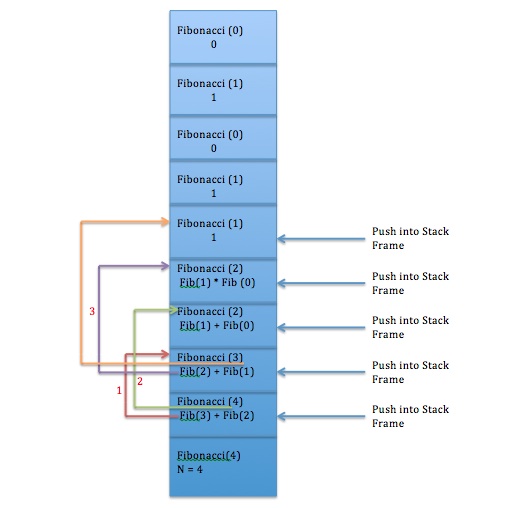
Now the call stack looks as follows, memory layout of call stack for a given recursive call of fibonacci program.
Let us analyse this example ,
If we observe the callstack , fib(2) , Fib(1) and Fib(0) called multiple times, which is not necessary as the value will be calculated .
For input n = 4 , the total number of times the fibonacci method called = 10.
Now let us take few more inputs and check how many times the function is getting called.
n = 5 => 16 times,
n = 6 => 26 times ,
If I generalise the number of time the function called will give us an astonishing result ,
number of times fib function calls = (2^n – C), Where C is constant, and very less ~ 2^n
Let us take some interesting inputs 🙂
n = 30 => 2692538 times
n = 31 => 4356618 times (just by increasing n by 1 , the number of times function called became so huge)
n = 42 => 866988874 times , Unbelievable !!! These results shows how recursive method is dangerous in this case.
n = 43 => my program not even stopping , even after 5 minutes .
Let us look on iterative method
long int fibonacciIteration(int n) {
int x = 0, y = 1, z = 1;
for (int i = 0; i < n; i++) {
x = y;
y = z;
z = x + y;
}
return x;
}
This method will return , fibonacci value within few seconds even if input n = 100 .
Conclusion is , selecting between iterative and recursive methods should be decided based on the problem statement, the problem looks simple with simple inputs, but analysing the problem with bigger inputs will actually shows the big picture .
Update: Complexity of recursive Fibonacci –
The recursive equation for this algorithm is T(n)=T(n−1)+T(n−2)+Θ(1)
For this it will be T(n)=Θ(ϕn)
where ϕ is the golden ratio (ϕ=(1+5√) / 2).
I strongly recommend to read Introduction to Algorithms 3rd edition : Purchase in FlipKart
A Video Tutorial on Analysis Of Recursive Function For Fibonacci is here
How string copy becomes costly – An Analysis
Let us try an interesting example , a simple but an interesting analysis at the end. Let me start with a requirement by taking an example .
Assume that you are getting ‘ N ‘ number of strings from an xml file , where ‘ N ‘ is really huge. Each string is again having too many characters. A library is being used to parse the strings from the xml file, library will return the strings one by one.
The library returns string and the length of the string in a callback method, our program has to copy the string to keep a copy of it.
Let me write a simple code for this , to make the code simple for better understanding I will avoid library usage and all other stuff. Just let us focus of core problem , that is copying ‘ N ‘ strings.
int main(){
getStrings();
return 1;
}
void getStrings(){
int numberOfCharacters = 2014; // this length will be returned by Library after parsing xml file
char *string1 = (char*)malloc(numberOfCharacters); // to hold string
strcpy(string1,"This string we will get from library, for this example we are hard coding it");
char *string2 = (char*)malloc(numberOfCharacters); // to hold string
strcpy(string2,string1); // have a copy of string returned by library .
}
The above problem looks very simple, but the last strcpy() call will become costly for you since number of strings are too big.
How strcpy is costly ?
strcpy typically looks like below –
char* strcpy(char * string1, const char * string2){
char * originalStringPointer = string1;
while(*string2 != '\0'){
*string1++ = *string2++;
}
*string1 = '\0';
return originalStringPointer;
}
So behind the screen for every string copy ( for all your N strings, where N is too big ) , strcpy method iterates each character and copies .
Let us take one example and analyse this –
Analysis I –
If I have 100 strings all of same length say 10
then the number of times the loop in strcpy runs is
100 * 10 = 1000 times, this doesn’t make much difference .
Analysis II –
Let us take bigger value ,
If I have 3000 strings of length 100 each
then your loop in strcpy runs 3000 * 100 = 3,00,000 times
3,00,000 times is big, also we assumes all strings are of same size and that is just 100, but in realworld example that might be different again.
So in such a scenario your strcpy becomes very costly for you, your application performs really bad that too if you didn’t handle this case properly. If by chance you are reading all the strings during the app launch, your application takes several seconds to show the first screen.
A clever programmer finds a better way to achieve this with better way.
Better approach for better performance –
If you observe the problem statement, just notice that we have a string and its length both. so instead of using strcpy we can go for memcpy which actually just transfers chunk of data from one location to another location rather than copying it character by character.
so just replacing strcpy() by memcpy() avoids 3,00,000 loop executions in your second analysis .
your getStrings method looks like below now
void getStrings(){
int numberOfCharacters = 2014; // this length will be returned by Library after parsing xml file
char *string1 = (char*)malloc(numberOfCharacters); // to hold string
strcpy(string1,"This string we will get from library, for this example we are hard coding it");
char *string2 = (char*)malloc(numberOfCharacters); // to hold string
memcpy(string2,string1,numberOfCharacters); // have a copy with memcpy.
}
It is always a very good practice to find best possible way to do something, even a one line code which runs hundreds, thousands of times will become bottleneck.