How Longitude, Latitude and GPS location services works
This article is to understand the mathematics behind GPS location services, how exactly google maps calculates the distance, how basic mathematics being used behind the screen.
Before going directly to mathematical part of it, let us understand the theory part 🙂 . how it is possible to locate places on the planet earth and calculate the distance? Mathematics has changed the world and is the base for everything. We all know that earth is like sphere, its not exact sphere because earth is spinning on its axis and the equator is flat compared to poles of the earth.
The image above clearly shows how exactly the earth is, since its flat along the equator the radius at equator is more compared to radius along the poles.
But considering the mean radius of earth we shall assume earth as a perfect sphere. So the radius of the earth is 6371Kms.
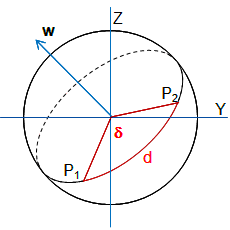
Let us consider two locations JP Nagar, and Jayanagar in Bangalore India. If I locate these places on the sphere It looks as below.
Mathematics behind Distance calculation using Locations points
Google Maps behind the screen uses Great Circle Distance Formula, and for using latitude and longitude the there is a popular formula called Hoversine formula.

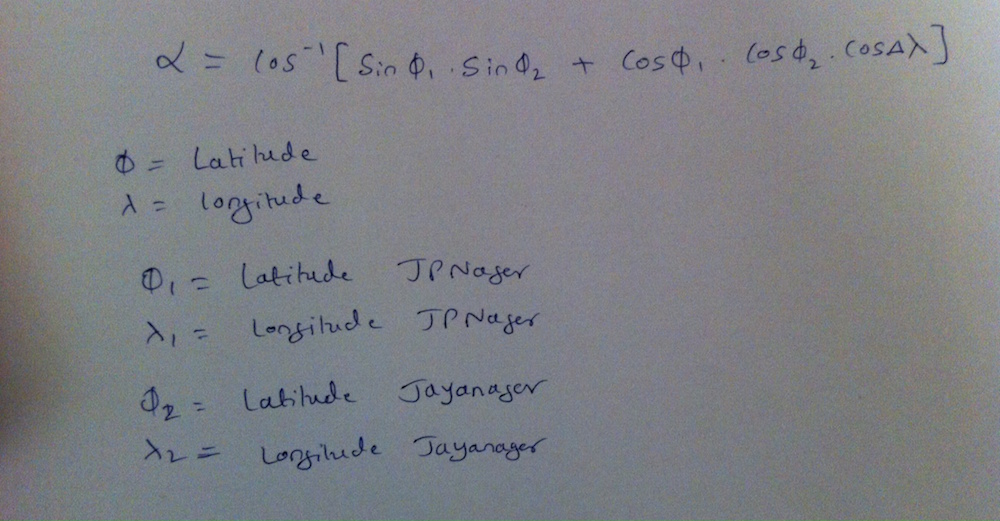
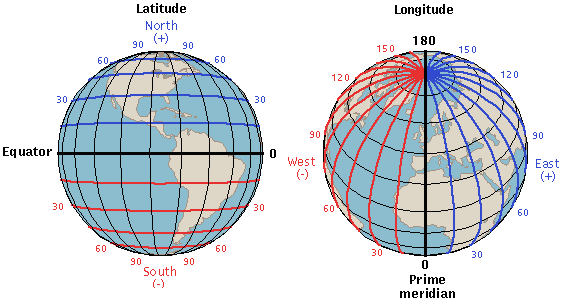
There are many methods to calculate the distance between two points, many will prefer the below logic. Note here the first image show all Latitude values vary between [-90,+90] and longitude varies between [-180,+180]
Also Read : An Interesting article one how Facebook trying to connect the world
Calculating Distance between two locations using Longitude and Latitude
//Earth radius is
static final double earthRadius = 6371; //Kilometers
double dLat = Math.toRadians(lat2 - lat1);
double dLng = Math.toRadians(lng2 - lng1);
double sindLat = Math.sin(dLat / 2);
double sindLng = Math.sin(dLng / 2);
double a = Math.pow(sindLat, 2)
+ Math.pow(sindLng, 2) * Math.cos(Math.toRadians(lat1)) * Math.cos(Math.toRadians(lat2));
double c = 2 * Math.atan2(Math.sqrt(a), Math.sqrt(1 - a));
double dist = earthRadius * c;
return dist;
The above code gives you the distance between two locations on a sphere.
For More Details On Mathematical part – https://undergroundmathematics.org/trigonometry-compound-angles/the-great-circle-distance
